doi: 10.62486/latia202451
ORIGINAL
Exploration of regularities in bipartite graphs using GEOGEBRA software
Exploración de regularidades en grafos bipartitos con uso del software GEOGEBRA
Elisa Oliva1 *, Mathias Díaz1 *
1Universidad Nacional de San Juan. Argentina.
Cite as: Oliva E, Díaz M. Exploration of regularities in bipartite graphs using GEOGEBRA software. LatIA. 2024; 2:51. https://doi.org/10.62486/latia202451
Submitted: 05-01-2024 Revised: 10-03-2024 Accepted: 31-07-2024 Published: 01-08-2024
Editor: Prof.
Dr. Javier González Argote ![]()
ABSTRACT
A classroom proposal is presented to integrate contents of Graph Theory and Linear Algebra in complete bipartite graphs, linking adjacency and Laplacian matrices, the eigenvalues of graphs will be determined, applicable to connectivity concepts. Students will be given exploration activities working with GeoGebra software, starting from several particular cases, with table works and questionnaires to be completed, in order to determine patterns on the eigenvalues of adjacency and Laplacian matrices of complete bipartite graphs. The work with patterns will lead to the generalization process, to abstract properties from observation and experimentation on examples. This learning experience builds bridges between the concrete and the symbolic, and the student is initiated in research.
Keywords: Complete Bipartite Graph; Eigenvalues; Generalization.
RESUMEN
Se presenta una propuesta áulica para integrar contenidos de Teoría de Grafos y Álgebra Lineal en grafos bipartitos completos, vinculando matrices de adyacencia y Laplaciana, se determinarán los autovalores de grafos, aplicables a conceptos de conectividad. Se plantearán a los estudiantes, actividades de exploración trabajando con el software GeoGebra, partiendo de variados casos particulares, con trabajos de tablas y cuestionarios a completar, para que se llegue a determinar patrones sobre los autovalores de las matrices de adyacencia y Laplaciana de grafos bipartitos completos. El trabajo con patrones conducirá al proceso de generalización, a abstraer propiedades a partir de la observación y de la experimentación en ejemplos. Con método inductivo se realizará la demostración de regularidades observadas.Esta experiencia de aprendizaje, tiende puentes entre lo concreto y lo simbólico, y que el estudiante se inicie en investigación.
Palabras claves: Grafo Bipartito Completo; Autovalores; Generalización.
INTRODUCTION
The starting point of this presentation is the realization of activities linking research and classroom teaching activities. It is part of a research project of the UNSJ 2023-2024, which aims to:
To develop lines of research work in mathematics education that address the development of cognitive activities to find regularities, modeling with algebraic resources, and using new technologies.
To develop logical-mathematical thinking skills in students with activities involving generalization situations as a strategy for teaching problem-solving.
The main objective is to determine if the Laplacian Matrix associated with complete Bipartite Graphs, for different numbers of nodes presents regularity in its eigenvalues and then establish a link with the eigenvalues of the Adjacency Matrix, the process of exploration in an increasing way by increasing the number of nodes, will be done with the free software Geogebra.
Given the difficulty in achieving algebraic learning in students who are not specifically mathematics majors, Lesley and Freimman (2004) and Papic (2007) point to the exploration and generalization of patterns as an essential approach in mathematical work and a powerful means for the development of algebraic thinking, which is what is guided by the use of GeoGebra. The second step will guide the generalization processes for developing algebraic thinking.
UNESCO (2005): The incorporation of ICT in education has the function of being a means of communication, a channel of communication and exchange of knowledge and experiences, an instrument to process information, a source of resources, an instrument for administrative management, a playful medium and cognitive development. All this leads to a new way of elaborating a didactic unit and, therefore, of evaluating because the ways of teaching and learning change; the teacher is no longer the manager of knowledge but a guide that allows orienting the student in front of his learning, in this aspect, the student is the “protagonist of the class,” because he is the one who must be autonomous.
Specifically in the proposal of the present Learning Sequence, the study begins with the approach of exploration activities increasing in difficulty with the use of GeoGebra through its algebraic interfaces and CAS view, working gradually according to the number of vertices of the graph, generating a large number of matrices to which the eigenvalues must be found. Based on this material, it is possible to move on to the stage of analysis and subsequent search for patterns, which contribute to the generalization and formalization of mathematical conjectures.
GeoGebra is an easy-to-use dynamic mathematics software that allows the association of geometric and algebraic objects to solve complex situations. The software allows for creatively addressing mathematical problems in different areas of knowledge, such as science education, technology, engineering, and mathematics, creatively and originally, bringing innovation to teaching and learning, which motivates the students’ work.
It is worth mentioning that, for the development of this topic, the reader would only need to have previous knowledge about some notions of Linear Algebra, such as matrices, proper subspaces, characteristic polynomials, autovectors, and eigenvalues, basic concepts of Graph Theory, and minimal use of GeoGebra software.
This document is articulated in a theoretical framework that supports the proposal. This section presents definitions and properties around the essential notions applied throughout the article. This development consists of two parts: the first one shows the different cases that could be analyzed with the software, and the second one deals with how the analyzed and obtained in the first stage will lead to the formalization of the characteristics and properties of the eigenvalues of adjacency matrices and Laplacian matrices. Finally, the conclusions referring to this type of didactic experience are presented.
METHOD
The didactic proposal presented is framed in the Theory of Realistic Mathematics Education (RME), where the student’s learning process takes place at different levels; in this regard, Zolkower, B. and Pérez, S. (2012): “RME understands learning as a discontinuous process that involves increasing levels of structuring, abstraction, generalization and formalization” and the principles on which it is based are:
1) Phenomenological exploration: the search for significant and not pre-structured phenomena to develop the student’s intuitive notions that lead them to form mathematical objects.
2) The use of models and symbols: the development from these intuitive notions, informal and linked to contexts, of more formal mathematical notions in the process of progressive mathematization.
3) Using students’ constructions and productions: Since what students do by themselves is meaningful, using their constructions and productions during the teaching process is essential for them to learn to mathematize.
4) Interaction: In situations of interaction, the contributions of different students can be compared and contrasted, which allows them to reflect on the mathematical activity, both their own and that of others, considering the relative advantages of different models and forms of symbolization.
5) The interweaving of curricular axes and themes: it is essential to consider didactic sequences in their multiple interactions”. (Zolkower and Perez, 2012, p. 176).
Implementing technological resources in the classroom is relevant so that the student can be introduced to experimentation, discovery, reflection, and research through dynamic learning enabled by computer tools. From this point, Barreiro, Leonian, Marino, Pochulu, and Rodriguez (2017) state that:
If we go back to our present, we can think that this transition forces us to change our objectives, to put the focus on another place, valuable and demanding, where some calculations, graphs, accounts, etc., can be solved immediately by technology so that we go for more. (p.72)
The incorporation of the free software GeoGebra, as the technological tool that can respond to these tasks, is due to its free manipulation and potential as a mathematical program, providing a wide variety of work views, commands, and tools.
Lesley and Freimman (2004) and Papic (2007) point to the exploration and visualization of patterns as an essential proposal in mathematical work and a powerful means for the development of algebraic thinking, which is what is guided by the use of GeoGebra for the subsequent achievement of generalization of regularities in an algebraic solid work. Cañadas, Castro, and Molina (2010) state, from a semiotic perspective, that students generalize when they can identify a pattern from some instances and apply this common feature to other particular cases, which had not been considered so far.
The second step proposed is to lead to generalization processes, emphasizing the development of inductive reasoning, which allows the discovery of new knowledge using conjectures based on the observed regularity of particular cases. The inductive method is the basis of the positivist research paradigm since it is the only valid method for generating knowledge, starting from empirical evidence and wholly stripped of subjectivism.
Joshua, S. and Dupin, J. (2005) state that generalization is constructed thanks to the abstraction of essential invariants. The abstracted properties are relations between objects rather than objects, and decontextualization is the primary generalization process. The patterns found belong to the numerical and geometric domains.
Previous knowledge
A brief review of the key concepts that the student should keep in mind when working with this didactic proposal is presented.
Regarding Linear Algebra topics:
Sea A = (aij) Mnxn : is called:
Eigenvalue of A (Eigenvalue of A), to the number, for which the system
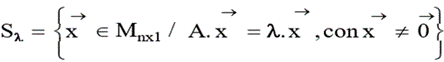
Eigen subspace of A corresponding to the eigenvalue to the set defined by:
· Characteristic Polynomial of A: to the polynomial P () = det (A - I)
· Characteristic Equation of A: det (A -I) = 0
· Spectrum of A (or spectral space): is the set of eigenvalues of A. Spectrum (A)
· If A is a diagonal matrix, its spectrum is the values located on the diagonal.
· Theorem: A is symmetric if and only if it is an orthogonally diagonalizable matrix.
· Theorem: a) A symmetric matrix with all its real elements has only real eigenvalues.
· Any two eigenvectors of a symmetric matrix A corresponding to two different eigenvalues are orthogonal.
Regarding Graph Theory:
Graphs allow the study of interrelationships between units that interact with each other. In mathematics and computer science, an undirected graph G = (V, E) is a pair formed by: V = {V1, V2, … , Vn} ≠ 0 (the elements of which are called vertices or nodes), is a symmetric binary relation (whose elements are called edges or axes).
For each undirected network G = (V, E) con |v| = n y |e| = m, can be defined:
The incidence matrix, which will be indicated with:
![]()
The adjacency matrix, which will be indicated with:
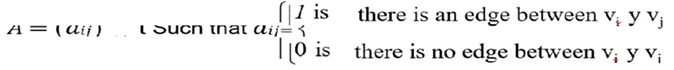
The Laplacian matrix, is defined as:
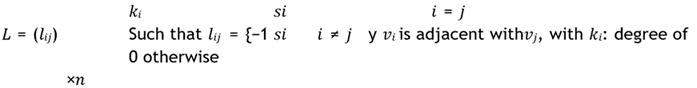
apex 𝑣𝑖.
Once the adjacency matrix is known, the alternative definition of the Laplacian matrix is as follows:

The Laplacian matrix also called the admittance matrix or Kirchhoff matrix, is another matrix representation of a graph used to study the spectral theory of graphs.
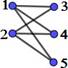
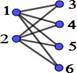
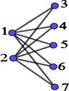
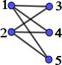
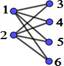
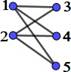
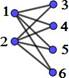
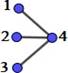
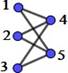
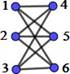
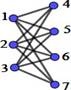
If, in addition, the vertex set V can be partitioned into two sets A and B, such that V=A∪B y A∩B=f, edges can only connect vertices of one set with vertices of the other set; this is formally: "x1,x2Î A; "y1,y2Î B; no there is no edge e=(x1,x2) ni e=(y1,y2), then the graph G=(V,E) is called a bipartite graph.
A complete bipartite graph is a bipartite graph in which all vertices of one subset are related to all vertices of the other subset.
Yes |𝑉| = 𝑛 + 𝑚, y |𝐴| = 𝑛 , |𝐵| = 𝑚, to grafo bipartito completo is indicated∶ 𝑲𝒏, 𝒎
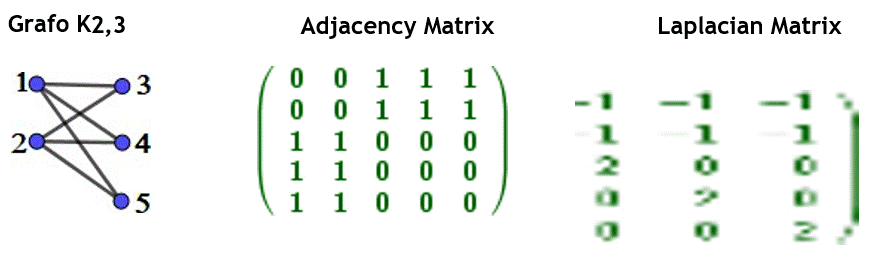
Figure 1. Laplacian and graph adjacency matrices K2,m
First stage: Exploration with geogebra
The classroom experience begins with the filling out of lists from what has been obtained with the software:
1. ACTIVITY: “Complete the three information tables of the K2, m graphs.”
· With the help of GeoGebra software, generate the Laplacian and adjacency matrices of the complete bipartite graphs for m=1, m=2, m=3, m=4, m=5, and obtain the eigenvalues associated with both matrices.
· Observing what has been obtained above, write conjectures about the Laplacian matrices and their eigenvalues for any value of “m.”
· Observing what has been obtained above, write conjectures about adjacency matrices and their eigenvalues for any value of “m”. With the help of GeoGebra software, verify that the given ones are eigenvectors. Generate examples of eigenvectors and write conjectures for any value of “m”.
Activities to work in groups, in a computer lab, or individually.
|
Table 1. Laplacian and graph adjacency matrices K2,m |
|||||
|
Graph K2,m |
Laplacian Matrix |
Proprietary Values |
Adjacency Matrix |
Proprietary Values |
Graph |
|
m=1 |
|
{0, 3, 1} |
|
{0, Ö2, -Ö2} |
|
|
m=2 |
|
{0, 4, 2, 2} |
|
{0, 0, 2, -2} |
|
|
m=3 |
|
{0, 6, 4, 2, 2, 2} |
|
{0, 0, 0, Ö6, -Ö6} |
|
|
m=4 |
|
|
|
|
|
|
m=5 |
|
|
|
|
|
|
Table 2. Eigenvectors of Laplacian Matrices of graphs K2,m |
||||
|
Graph K2,m |
Laplacian Matrix |
Own Vector |
Own Vector |
Own Vector |
|
|
|
1 (1) 1 |
−1 (−1) −1 |
|
|
|
|
1 (1) 1 1 |
|
2 (2) 2 2 |
|
|
|
1 1 1 1 (1) |
|
|
|
|
|
|
|
|
|
Table 3. Eigenvectors of Laplacian Matrices of graphs K2,m |
||||
|
Graph K2,m |
Laplacian Matrix |
Own Vector |
Own Vector |
Own Vector |
|
|
|
1 |
−1 |
|
|
(−1) |
( 1 ) |
|||
|
0 |
0 |
|||
|
|
|
1 |
|
2 |
|
(−1) |
(−2) |
|||
|
0 |
0 |
|||
|
0 |
0 |
|||
|
|
|
1 −1 0 0 ( 0 ) |
|
|
|
|
|
1 −1 0 0 0 ( 0 ) |
|
|
2. ACTIVITY: “Complete the information tables of the K3, m networks”
· With the help of GeoGebra software, generate the Laplacian and adjacency matrices of the complete bipartite graphs for m=1, m=2, m=3, m=4, m=5, and obtain the eigenvalues associated with both matrices.
· Observing what has been obtained above, write conjectures about the Laplacian matrices and their eigenvalues for any value of “m.”
· Observing what is obtained above, write conjectures about the adjacency matrices and the associated eigenvalues for any value of “m.” With the help of GeoGebra software, verify that the given ones are eigenvectors. Generate examples of eigenvectors and write conjectures for any value of “m”.
Activities to be worked on in groups, in a computer lab, or individually.
|
Table 4. Laplacian and graph adjacency matrices K3,m |
|||||
|
Graph K3,m |
Laplacian Matrix |
Proprietary Values |
Adjacency Matrix |
Proprietary Values |
Graph |
|
m=1 |
|
{0, 4, 1, 1} |
|
|
|
|
m=2 |
|
{0, 5, 3, 2, 2} |
|
|
|
|
m=3 |
|
{0, 6, 3, 3, 3, 3} |
|
|
|
|
m=4 |
|
|
|
|
|
3. ACTIVITY: generate table 3, (idem what has been done in table 2), that allows the study of Eigenvectors of Laplacian Matrices of K3,m graphs.
4. ACTIVITY: generate table 4, (idem what was done in table 3), that allows the study of Eigenvectors of Adjacency Matrices of K3,m graphs.
The use of the technological resource Geogebra applied to the teaching-learning process of mathematics; its importance lies in the fact that it is a dynamic tool that allows the student to gain time to make multiple trials in the time of only one development made with pencil and paper, this provides an analytical capacity, significantly improves motivation in students and at the same time promotes autonomy in them in educational contexts Coloma (2020), Zabala (2012), Real (2013).
Sinclair and Yurita (2008) researched how ICT improves conjectures and reasoning in any problem. Alemán de Sánchez (2002) points out the theoretical advantages of using ICT in mathematics. A competence that the student must develop is: “Information processing and digital competence”.
5. ACTIVITY: “Generate and complete information tables of the K4,m networks” (similar to those worked in the previous activities).
RESULTS
As it is an activity in development, it is proposed how the student is expected to reach the expected results:
Part Two: Elaboration of conjectures
Process 1: this is the stage of searching for patterns from the analysis of conjectures based on what has been collected in the previous tables; the work on the eigenvalues of Laplacian matrices begins.
1. ACTIVITY: to work on conjectures of the visualized eigenvalues of the Laplacian matrix of K2, m.
· Is “zero” the eigenvalue of the K2, m Laplacian matrices with what algebraic multiplicity?
· Is there any other eigenvalue different from the previous ones? Can its value be linked to something found? What multiplicity does it have?
· Does any eigenvalue have any relation with the size of the matrix?
· Indicate all the eigenvalues of the Laplacian matrices of K2,6; K2,7, y K2,8
2. ACTIVITY: to work on conjectures from the visualized eigenvalues of the adjacency matrix of K3, m
· Are “m” ,“m+3” ,“three”: eigenvalues of the adjacency matrices of K3, m with what algebraic multiplicity?
· Are there any eigenvalues other than the above?
· What is the sum of the non-zero components for the eigenvectors you worked on?
· How are the null and non-zero components arranged in the eigenvector?
3. ACTIVITY: propose work similar to the two previous activities to respond with the visualized in the eigenvalues of the Laplacian matrix of K4, m.
Process 2: pattern search stage from the analysis of conjectures, based on the information gathered in the previous tables, work begins on the eigenvalues of the adjacency matrix.
1. ACTIVITY: to work on conjectures of what is visualized in the eigenvalues of the adjacency matrix of K2, m.
· Are “zero” ,“√𝟐. 𝒎”, “-√𝟐. 𝒎”: eigenvalues of the adjacency matrices of K2, m with what algebraic multiplicity?
· Are there any eigenvalues other than the above?
· What is the sum of the non-zero components for the eigenvectors you worked on?
· How are the null and non-zero components arranged in the eigenvector?
2. ACTIVITY: to work on conjectures from the visualized eigenvalues of the adjacency matrix of K3, m
· Are “zero” ,“√𝟑. 𝒎” ,“-√𝟑. 𝒎”: eigenvalues of the adjacency matrices of K3, m with what algebraic multiplicity?
· Are there any eigenvalues other than the above?
· What is the sum of the non-zero components for the eigenvectors you worked on?
· How are the null and non-zero components arranged in the eigenvector?
3. ACTIVIDAD: based on the two previous tasks, make conjectures from the visualized eigenvalues of the adjacency matrix of K4, m.
Part Three: Generalization of Conjunctions with Respect to Laplacian Matrixes
Process 1: generalization of the conjectures, demonstration of some patterns based on what has been collected in the previous stage, work begins on the eigenvalue of the Laplacian matrix of Kn, m.
· Suggestion to use the observation on the structure of the rows of the Laplacian matrix and conclusions of point 8) of the preceding activities.
Process 2: generalization of conjectures, proof that zero is the eigenvalue of the adjacency matrix of Kn, m.
· Suggestion to build a general format of the eigenvector, as shown in tables 2, 3; from the preceding activities and prove that it is an eigenvector.
Future applications
Calculate the energy of a graph (Cubria, 2018) by using the Laplacian Matrix or the Adjacency Matrix and establishing links with the number of axes of the graph.
CONCLUSIONS
The experience developed will allow students to share something they have created or discovered. Giving specific time for that stage of communication encourages concentration, and the deductions of their peers can inspire them, and they will find value in their work (Eady & Lockyer, 2018). In this context, it is inferred that often, students who do not excel in traditional classes do not have the opportunity to receive much praise. Therefore, technology changes that environment, providing opportunities for all students to shine, including introverts and those who may lack proficiency in certain subjects by sharing their ideas in classes. ICT integration in mathematics is needed to motivate students, make classes more innovative, promote autonomous learning, and make encounters more rewarding.
The experience presented here provides a wide range of advantages, detailed below:
Advantages of the use of software in teaching and learning
· It benefits students by giving primacy to thinking processes over manual processes, such as pencil and paper, so that they can investigate and construct mathematical knowledge.
· In principle, it is convenient to work with manipulative material rather than simply mathematical software to reduce the volume of calculations by hand before moving on to the arithmetic-algebraic plane.
· Working with GeoGebra is an excellent academic support, achieving a significant improvement in the traditional scenario of the learning process, adapted to a contextualized problem.
Advantages of algebraic work, in the teaching-learning process
· Working with patterns and regularities encourages the development of different points of view to approach a problem, shows that finding an approach does not imply that it is concluded, and even allows the generation of new problems that it is concluded, and even allows the generation of new problems. It leads to recognizing the value of algebraic language, both to express variables and to validate conjectures, relying on the rules of script transformation.
· Working with patterns leads to making conjectures, symbolizing them, and then, in the generalization process, demonstrating them and applying them in solutions and results to other problems.
REFERENCES BIBLIOGRAPHICS
1. Alemán de Sánchez, A. (2002). La enseñanza de la matemática asistida por computador. Recuperado en Julio de 2019 de: https://es.scribd.com/document/7795982/La–Tecnologia–y–La–Mat
2. Castro, E., Cañadas, M. C. y Molina, M. (2010). El razonamiento inductivo como generador de conocimiento matemático. UNO, 54. Recuperado de: http://digibug.ugr.es/bitstream/10481/26079/6/Uno-54-_2010.pdf
3. Coloma, M. L. (2020). Las Tics como herramienta metodológica en matemática. Revista ESPACIOS Vol. 41 (11) , 1-9. Recuperado el 6 de 08 de 2020, de http://www.academia.edu/download/62945190/Articulo_Espacios_TICS20200413- 81578- 14jzkam.pdf
4. Cubria, F(2018). Energía de matrices. Tesis de maestría. Recuperado en Noviembre de 2023 de: https://www.fing.edu.uy/imerl/grupos/gia/pdf/fcubria_mas.pdf
5. Eady M., Lockyer L. (2018). Technology and teachingstrategies. Tools forlearning, vol 23. N° 4.
6. Herrera M., Izquierdo J., Pérez - García R. y Ayala-Cabrera D. La regularización del grafo de la red de abastecimiento de agua para la propuesta de su sectorización. ResearchGate. Recuperado de https://www.researchgate.net/publication/288965452_La_regularizacion_del_grafo_de_la_red_de_abastecimiento_de_agua_para_la_propuesta_de_su_sectorizacion
7. Joshua, J y Dupin, J. (2005). Introducción a la didáctica de las ciencias y de la matemática. Buenos Aires. Colihue.
8. Lesley L., Freiman V. (2004). Tracking primary student ś understanding of patterns. In Proceeeding of the 28thConference of the International Group for the Psychology of Mathematics Education (Vol. 2, pp. 415-422). Norway. PME.
9. Mañas, J. (2013). Utilización de las tic en el aula. GeoGebra y wiris. (Tesis de maestría). Universidad de Almería, España. Recuperado de http://repositorio.ual.es/bitstream/handle/10835/2289/Trabajo.pdf?sequence=1
10. Papic M. (2007). Promotting repeating patterns with Young children-more than just alternating colours. AustralianPrimaryMathemathicsClassroom, 12(1), 8.
11. Pochulu M. y Rodríguez M. (2016). Educación Matemática. Aportes a la formación docente desde distintos enfoques teóricos. Los Polvorines, Argentina. UNGS. Radford, L. (2013). En torno a tres problemas de la generalización. En: L. R.ico
12. M. C. Cañadas,J. Gutiérrez, M. Molina y I. Segovia (Eds.). Investigación en Didáctica de la Matemática. España: Editorial Comares.
13. Rangel Álvarez, L (2012) Patrones y Regularidades Numéricas: Razonamiento Inductivo. Universidad Nacional de Colombia, Colombia.
14. Real, M. (2013). Las TIC en el proceso de enseñanza y aprendizaje de las matemáticas. personal.us.es, 1-13. Recuperado el 3 de 08 de 2020, de https://personal.us.es/suarez/ficheros/tic_matematicas.pdf
15. Rodríguez, M. (2017). Criterios para valorar el uso de nuevas tecnologías en la clase de matemática. En P. Barreiro, P. Leonian, T. Marino, M. Pochulu y M. Rodríguez (Eds.), Perspectivas metodológicas en la enseñanza y en la investigación en educación matemática. (pp. 71 - 94). Los Polvorines, Argentina. UNGS.
16. Sinclair, N. y Yurita, V.(2008). To be or to become: How Dynamic geometry changes discourse. Research in: Mathematics Education, 10, 135-150.
17. UNESCO (2005). Formación docente y las tecnologías de Información y Comunicación, Santiago.
18. Zabala, S. Z. (2012). Pedagogía Informacional: Nuevo paradigma para educar en la sociedad de la información. recursos.portaleducoas.org, 1-18. Recuperado el 2 de 08 de 2020, de https://recursos.portaleducoas.org/sites/default/files/1757.pdf
19. Bhagat, P. K., Choudhary, P., & Singh, Kh. M. (2021). A novel approach based on fully connected weighted bipartite graph for zero-shot learning problems. Journal of Ambient Intelligence and Humanized Computing, 12(9), 8647–8662. https://doi.org/10.1007/s12652-020-02615-6
20. Blöcker, C., & Rosvall, M. (2020). Mapping flows on bipartite networks. Physical Review E, 102(5), 052305. https://doi.org/10.1103/PhysRevE.102.052305
21. Chakraborty, B., & Mandal, M. (2022). Regularity of symbolic powers of certain graphs (arXiv:2203.08572). arXiv. https://doi.org/10.48550/arXiv.2203.08572
22. Dung, L. X., Hien, T. T., Nguyen, H. D., & Trung, T. N. (2021). Regularity and Koszul property of symbolic powers of monomial ideals. Mathematische Zeitschrift, 298(3), 1487–1522. https://doi.org/10.1007/s00209-020-02657-8
23. Emadi Kouchak, M. M., Safaei, F., & Reshadi, M. (2023). Graph entropies-graph energies indices for quantifying network structural irregularity. The Journal of Supercomputing, 79(2), 1705–1749. https://doi.org/10.1007/s11227-022-04724-9
24. Habib, M., Mouatadid, L., Sopena, É., & Zou, M. (2024). (𝜶,𝜷)—Modules in Graphs. SIAM Journal on Discrete Mathematics, 38(1), 566–589. https://doi.org/10.1137/21M1443534
25. Habib, M., Mouatadid, L., & Zou, M. (2020). Approximating Modular Decomposition Is Hard. In M. Changat & S. Das (Eds.), Algorithms and Discrete Applied Mathematics (pp. 53–66). Springer International Publishing. https://doi.org/10.1007/978-3-030-39219-2_5
26. Hang, N. T., & Hien, T. T. (2023). Regularity of powers of cover ideals of bipartite graphs. International Journal of Algebra and Computation, 33(02), 317–335. https://doi.org/10.1142/S0218196723500169
27. Jin, Y., Zhang, W., He, X., Wang, X., & Wang, X. (2020). Syndrome-aware Herb Recommendation with Multi-Graph Convolution Network. 2020 IEEE 36th International Conference on Data Engineering (ICDE), 145–156. https://doi.org/10.1109/ICDE48307.2020.00020
28. Koley, M., & Römer, T. (2022). Seminormality, canonical modules, and regularity of cut polytopes. Journal of Pure and Applied Algebra, 226(1), 106797. https://doi.org/10.1016/j.jpaa.2021.106797
29. Lin, R. (2021). Conditional matching preclusion for regular bipartite graphs and their Cartesian product. Discrete Applied Mathematics, 299, 17–25. https://doi.org/10.1016/j.dam.2021.04.011
30. Megias, D., Alatrista Salas, H., Salas, J., Maehara Aliaga, Y., & Núñez del Prado, M. (2022). A graph-based differentially private algorithm for mining frequent sequential patterns. https://doi.org/10.3390/app12042131
31. Nandi, R., & Nanduri, R. (2022). On regularity bounds and linear resolutions of toric algebras of graphs. Journal of Commutative Algebra, 14(2), 285–296. https://doi.org/10.1216/jca.2022.14.285
32. Nandi, R., & Nanduri, R. (2023). On regularity of Rees algebras of edge ideals of cone graphs. Indian Journal of Pure and Applied Mathematics, 54(1), 28–37. https://doi.org/10.1007/s13226-022-00226-9
33. Nanduri, R. (2022). On regularity of symbolic Rees algebras and symbolic powers of vertex cover ideals of graphs. Proceedings of the American Mathematical Society, 150(5), 1955–1965. https://doi.org/10.1090/proc/15824
34. Neves, J. (2020). Regularity of the vanishing ideal over a bipartite nested ear decomposition. Journal of Algebra and Its Applications, 19(07), 2050126. https://doi.org/10.1142/S0219498820501261
35. Neves, J., Vaz Pinto, M., & Villarreal, R. H. (2020). Joins, ears and Castelnuovo–Mumford regularity. Journal of Algebra, 560, 67–88. https://doi.org/10.1016/j.jalgebra.2020.05.014
36. Nunez-del-Prado, M., Maehara-Aliaga, Y., Salas, J., Alatrista-Salas, H., & Megías, D. (2022). A Graph-Based Differentially Private Algorithm for Mining Frequent Sequential Patterns. Applied Sciences, 12(4), Article 4. https://doi.org/10.3390/app12042131
37. Shen, Y.-H., & Zhu, G. (2023). Powers of generalized binomial edge ideals of path graphs (arXiv:2310.20235). arXiv. https://doi.org/10.48550/arXiv.2310.20235
38. Wang, H., & Tang, Z. (2023). Regularity of powers of binomial edge ideals of complete multipartite graphs. Czechoslovak Mathematical Journal, 73(3), 793–810. https://doi.org/10.21136/CMJ.2023.0246-22
39. Wu, Y., Yin, Z., Zhou, K., Wang, R., Yang, Y., Yin, Z., Ruan, C., & Zhang, Y. (2021). A Hybrid-scales Graph Contrastive learning Framework for Discovering Regularities in Traditional Chinese Medicine Formula. 2021 IEEE International Conference on Bioinformatics and Biomedicine (BIBM), 1104–1111. https://doi.org/10.1109/BIBM52615.2021.9669658
40. Zhang, X., Wang, H., Yu, J., Chen, C., Wang, X., & Zhang, W. (2022). Polarity-based graph neural network for sign prediction in signed bipartite graphs. World Wide Web, 25(2), 471–487. https://doi.org/10.1007/s11280-022-01015-4
FINANCING
None.
CONFLICT OF INTEREST
None.
AUTORSHIP CONTRIBUTION
Conceptualization: Elisa Oliva, Mathias Díaz.
Data curation: Elisa Oliva, Mathias Díaz.
Formal analysis: Elisa Oliva, Mathias Díaz.
Research: Elisa Oliva, Mathias Díaz.
Writing - original draft: Elisa Oliva, Mathias Díaz.
Writing - proofreading and editing: Elisa Oliva, Mathias Díaz.