ORIGINAL

Exploration of regularities in bipartite graphs using GEOGEBRA software

Exploración de regularidades en grafos bipartitos con uso del software GEOGEBRA

Elisa Oliva¹ *, Mathias Díaz¹ *

¹Universidad Nacional de San Juan. Argentina.

Citar como: Oliva E, Díaz M. Exploration of regularities in bipartite graphs using GEOGEBRA software. LatIA. 2024; 2:51. https://doi.org/10.62486/latia202451

Enviado: 05-01-2024 Revisado: 10-03-2024 Aceptado: 31-07-2024 Publicado: 01-08-2024

Editor: Prof. Dr. Javier González Argote

ABSTRACT

A classroom proposal is presented to integrate contents of Graph Theory and Linear Algebra in complete bipartite graphs, linking adjacency and Laplacian matrices, the eigenvalues of graphs will be determined, applicable to connectivity concepts. Students will be given exploration activities working with GeoGebra software, starting from several particular cases, with table works and questionnaires to be completed, in order to determine patterns on the eigenvalues of adjacency and Laplacian matrices of complete bipartite graphs. The work with patterns will lead to the generalization process, to abstract properties from observation and experimentation on examples. This learning experience builds bridges between the concrete and the symbolic, and the student is initiated in research.

Keywords: Complete Bipartite Graph; Eigenvalues; Generalization.

RESUMEN

Se presenta una propuesta áulica para integrar contenidos de Teoría de Grafos y Álgebra Lineal en grafos bipartitos completos, vinculando matrices de adyacencia y Laplaciana, se determinarán los autovalores de grafos, aplicables a conceptos de conectividad. Se plantearán a los estudiantes, actividades de exploración trabajando con el software GeoGebra, partiendo de variados casos particulares, con trabajos de tablas y cuestionarios a completar, para que se llegue a determinar patrones sobre los autovalores de las matrices de adyacencia y Laplaciana de grafos bipartitos completos. El trabajo con patrones conducirá al proceso de generalización, a abstraer propiedades a partir de la observación y de la experimentación en ejemplos. Con método inductivo se realizará la demostración de regularidades observadas.Esta experiencia de aprendizaje, tiende puentes entre lo concreto y lo simbólico, y que el estudiante se inicie en investigación.

Palabras claves: Grafo Bipartito Completo; Autovalores; Generalización.

INTRODUCCIÓN

Esta presentacióntiene como punto de partidala realización de actividades de vinculación entre la investigación y la actividad docente áulica. Se enmarca en un proyecto de investigación de la UNSJ 2023-2024, que tiene por objetivos:

· Desarrollar líneas de trabajo de investigación en Educación Matemática que aborden el desarrollo de actividades cognitivas para hallar regularidades, con modelación con recursos algebraicos, y uso de Nuevas Tecnologías

· Desarrollar habilidades de pensamiento lógico - matemático en los estudiantes con actividades que involucren situaciones de generalización como estrategia para la enseñanza – aprendizaje de resolución de problemas.

El objetivo principal radica en determinar si la Matriz Laplaciana asociada a Grafos Bipartitos completos, para distinto número de nodos, presenta regularidad en sus autovalores, y luego establecer vínculo con los autovalores de la Matriz de Adyacencia, el proceso de exploración en forma creciente por aumento del número de nodos, se realizará con el software libre Geogebra.

Ante la dificultad en el logro de aprendizajes algebraicos en estudiantes que no son de carreras específicamente de matemática, Lesley y Freimman (2004) y Papic (2007) señalan la exploración y generalización de patrones como una propuesta esencial en el trabajo matemático y un potente medio para el desarrollo del pensamiento algebraico, lo cual es lo que se guía con el uso de GeoGebra. El segundo paso será orientar los procesos de generalización para el desarrollo del pensamiento algebraico.

UNESCO (2005): la incorporación de las TIC en educación tiene como función ser un medio de comunicación, canal de comunicación e intercambio de conocimiento y experiencias, instrumentos para procesar la información, fuente de recursos, instrumento para la gestión administrativa, medio lúdico y desarrollo cognitivo. Todo esto conlleva a una nueva forma de elaborar una unidad didáctica y por ende de evaluar, debido a que las formas de enseñanza y aprendizaje cambian, el profesor ya no es el gestor del conocimiento sino que un guía que permite orientar al alumno frente su aprendizaje, en este aspecto, el alumno es el “protagonista de la clase”, debido a que es él quien debe ser autónomo.

Específicamente en la propuesta de la presente Secuencia de Aprendizaje, se inicia el estudio con el planteo de actividades de exploración crecientes en dificultad con uso de GeoGebra a través de sus interfaces algebraica y vista CAS, trabajando en forma gradualsegún el número de vértices del grafo, generandoun gran número de matrices a las que se les deberán hallar los autovalores. En base a este material se puedepasar a la etapa de análisis y posterior búsqueda de patrones, que contribuyan a la generalización y formalización de conjeturas matemáticas.

GeoGebra es un software de matemática dinámica, fácil de usar, y que ofrece la posibilidad de asociar objetos geométricos y algebraicos para resolver situaciones complejas. El software permite abordar problemas matemáticos de distintas áreas del saber: educación en ciencias, tecnología, ingeniería y matemáticas, en forma creativa y original, aportando innovación a la enseñanza y el aprendizaje, lo cual motiva el trabajo del estudiante.

Cabe destacar que, para el desarrollo de la presente temática solo requeriría que el lector cuentecon conocimientos previos sobre algunas nociones de Álgebra Lineal, tales como: matrices, subespacios propios, polinomios característicos, autovectores y autovalores,conceptos básicos de la Teoría de Grafos, y un manejo mínimo del software GeoGebra.

Este documento se articula en un marco teórico que fundamenta la propuesta, una sección quepresenta definiciones y propiedades en torno a las nociones imprescindibles que se aplican a lo largo delartículo, un desarrollo que consta de dos partes: la primera, muestra los distintos casos que se podrían analizar con el software y la segunda, trata sobre cómo lo analizado y obtenido en la primer etapa, va a conducir a la formalización de las características y propiedades de los autovalores de matrices de adyacencia y laplacianas. Finalmente, se exponen las conclusiones referidas a este tipo de experiencias didácticas.

MÉTODO

La propuesta didácticaque se presentaestá enmarcada en la Teoría de EducaciónMatemática Realista (EMR), donde el proceso de aprendizaje del alumno se realiza en distintos niveles; al respecto, Zolkower, B. y Pérez, S. (2012): “La EMR entiende al aprendizaje como un proceso discontinuo que involucra niveles crecientes de estructuración, abstracción, generalización y formalización” y los principios en que se basa son:

· La exploración fenomenológica: la búsqueda de fenómenos significativos y no pre-estructurados con vías de desarrollar en los alumnos nociones intuitivas que los lleven a la formación de objetos matemáticos.

· El uso de modelos y símbolos: el desarrollo a partir de estas nociones intuitivas, informales y ligadas a contextos, de nociones matemáticas más formales en un proceso de matematización progresiva.

· El uso de construcciones y producciones de los alumnos: dado que lo que los alumnos hacen por si mismos es significativo para ellos, hacer uso de sus construcciones y producciones durante los procesos de enseñanza es esencial para que estos aprendan a matematizar.

· La interacción: en situaciones de interacción, las contribuciones de diversos alumnos pueden ser comparadas y contrastadas lo cual les permite reflexionar acerca de la actividad matematizadora, tanto la propia como la de otros, considerando las ventajas relativas de los diferentes modelos y formas de simbolización.

· El entrecruzado de ejes y temas curriculares: es importante considerar a las secuencias didácticas en sus múltiples interacciones.” (Zolkower y Pérez, 2012, p. 176)

La implementación de recursos tecnológicos en el aula es relevante para que el estudiante pueda introducirse en actividades de experimentación, descubrimiento, reflexión, investigación a través de un aprendizaje dinámico que permiten las herramientas informáticas.Desde este punto, Barreiro, Leonian, Marino, Pochulu y Rodríguez (2017) afirman que:

Si volvemos a nuestro presente, podemos pensar que esta transición nos obliga a cambiar nuestros objetivos, a poner el foco en otro lugar, valioso y exigente, en donde algunos cálculos, gráficos, cuentas, etcétera, puedan ser resueltos inmediatamente por la tecnología para que vayamos por más. (p.72)

La incorporación del software libreGeoGebra, como la herramienta tecnológica que puede dar respuesta a estas tareas, se debe a su libre manipulación y potencialidad como programa matemático, brindando una amplia variedad de vistas de trabajo, comandos y herramientas.

Lesley y Freimman (2004) y Papic (2007) señalan a la exploración y visualización de patrones, como una propuesta esencial en el trabajo matemático y un potente medio para el desarrollo del pensamiento algebraico, lo cual es lo que se guía con el uso de GeoGebra; para el logro posterior de generalización de regularidades en un fuerte trabajo algebraico. Cañadas, Castro y Molina (2010) afirman, desde una perspectiva semiótica, que los estudiantes generalizan cuando tienen la capacidad de identificar un patrón, a partir de ciertos casos y también aplican esta característica común a otros casos particulares, que no se habían considerado hasta el momento.

El segundo paso que se plantea es conducir a lograr procesos de generalización haciendo énfasis en el desarrollo del razonamiento inductivo: que permite el descubrimiento de conocimiento nuevo, por medio de conjeturas basadas en la regularidad observada de casos particulares.El método inductivo es base del paradigma positivista de investigación, pues, al partir de evidencias empíricas, despojado por completo del subjetivismo, es el único válido para generar conocimientos.

Joshua, S. y Dupin, J.(2005); afirman que la generalización se construye gracias a la abstracción de invariantes esenciales. Las propiedades abstraídas son más bien relaciones entre objetos que objetos mismos, y la descontextualización es el proceso principal de la generalización. Los patrones hallados pertenecen al dominio: numérico y geométrico.

Saberes previos

Se presenta una breve revisión de los conceptos claves que deberá tener presente el estudiante al momento de trabajar esta propuesta didáctica.

Respecto a tópicos de Algebra Lineal:

Sea A = (aij) Mnxn: se llama:

· Autovalor de A (Valor Propio óeigenvalor de A), al número l, para el cual el sistema A. x=λx ; tiene una solución x≠0 . El vector solución x ∈ Mnx1 se llama autovector de A (Vector Propio de A óeigenvector de A), correspondiente al valor propio λ de A.

· Subespacio propio de A correspondiente al valor propio l al conjunto definido por:

· Polinomio Característico de A: al polinomio P (λ) = det (A – λI)

· Ecuación Característica de A: det (A - λI) = 0

· Espectro de A( o espacio espectral): es el conjunto de valores propios de A. Espectro (A) = {λ1,…, λp} p≤n ; y λi≠λj

· Si A es una matriz diagonal, su espectro son los valores ubicados en la diagonal.

· Teorema: A es simétrica si y solo si es una matriz ortogonalmente diagonalizable.

· Teorema:

1. Una matriz simétrica con todos sus elementos reales, solo tiene autovalores reales.

2. Dos autovectores cualesquiera de una matriz simétrica A que corresponden a dos autovalores diferentes, son ortogonales.

Respecto a teoría de Grafos:

Los grafos permiten estudiar las interrelaciones entre unidades que interactúan unas con otras. En matemática y ciencias de la computación, un grafo 𝑮 = (𝑽, 𝑬) no dirigido es un par formado por: 𝑉 = {𝑣₁, 𝑣₂, … , 𝑣_𝑛} ≠ ∅ (cuyos elementos se llaman vértices o nodos) y 𝐸 ⊆ 𝑉 × 𝑉, es una relación binaria simétrica (cuyos elementos se llaman aristas o ejes).

Para cada grafo no dirigido 𝑮 = (𝑽, 𝑬)con|𝑉| = 𝑛 y |𝐸| = 𝑚, se pueden definir:

La matriz de incidencia, que se indicará con:

La matriz de adyacencia, que se indicará con:

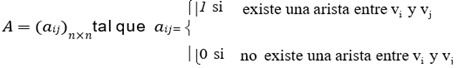
La matriz laplaciana, se define como:

Conocida la matriz de adyacencia, se tiene como definición alternativa de matriz laplaciana, la siguiente:

La matriz laplaciana, también denominada matriz de admitancia o matriz de Kirchhoff, es otra representación matricial de un grafo, que es usada para estudiar la teoría espectral de grafos.

Si además el conjunto de vértices V, se puede particionar en dos conjuntos A y B, tal que V=A∪B y A∩B=∅, de manera que las aristas sólo pueden conectar vértices de un conjunto con vértices del otro; esto es formalmente: ∀x1,x2∈A; ∀y1,y2∈B; no existe ninguna arista e=(x1,x2) ni e=(y1,y2), entonces el grafo G=(V,E) se llama grafo bipartito.

Un grafo bipartito completo es un grafo bipartito, en que todos los vértices de uno de los subconjuntos están relacionados con todos los del otro subconjunto.

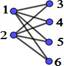
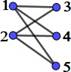
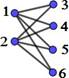
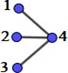
Si |𝑉| = 𝑛 + 𝑚, y |𝐴| = 𝑛 , |𝐵| = 𝑚, al grafo bipartido completo se lo indica con∶ 𝑲𝒏, 𝒎

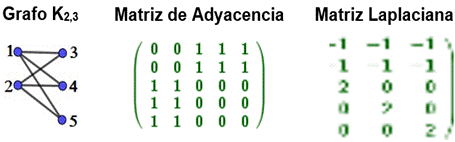
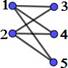
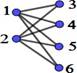
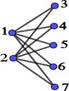
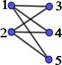
Figura 1. Matrices laplacianas y de adyacencia de grafos K2,m

Observación: estructura de las filas de la matriz Laplaciana: Cada fila tiene en la diagonal principal el grado del vértice, tantos elementos que valen “-1” como el grado del vértice y el resto de los elementos nulos.

Primer Etapa: Exploración con GEOGEBRA

La experiencia áulica, inicia con el llenado de listas desde lo obtenido con el software:

1. ACTIVIDAD: “Completar las tres tablas de información de los grafos K2,m”

· Con la ayuda del software GeoGebra, generar las matrices laplacianas y de adyacencia de los grafos bipartitos completos para m=1, m=2, m=3, m=4, m=5, obtengan los autovalores asociados a ambas matrices.

· Observando lo obtenido anteriormente, redactar conjeturas a cerca de las matrices de laplacianas y sus autovalores, para cualquier valor de “m”.

· Observando lo obtenido anteriormente, redactar conjeturas acerca de las matrices de adyacencia y los autovalores asociados a ellas, para cualquier valor de “m”.Verificar, con la ayuda del software GeoGebra, que son autovectores los dados.Generar ejemplos de autovectores y redactar conjeturas para cualquier valor de “m”.

Actividades a trabajar en grupos, en gabinete de informática; o individualmente.

Tabla 1. Matrices laplacianas y de adyacencia de grafos K2,m
Grafo K2,m	Matriz Laplaciana	Valores Propios	Matriz de Adyacencia	Valores Propios	Gráfica
m=1		{0, 3, 1}		{0, √2, -√2}
m=2		{0, 4, 2, 2}		{0, 0, 2, -2}
m=3		{0, 6, 4, 2, 2, 2}		{0, 0, 0, √6, -√6}
m=4
m=5

Tabla 2. Vectores propios de Matrices Laplacianas de grafos K2,m
Grafo K2,m	Matriz Laplaciana	Vector Propio	Vector Propio	Vector Propio
		1 (1) 1	−1 (−1) −1
		1 (1) 1 1		2 (2) 2 2
		1 1 1 1 (1)

Tabla 3. Vectores propios de Matrices Adyacencia de grafos K2,m
Grafo K2,m	Matriz Adyacencia	Vector Propio	Vector Propio	Vector Propio
		1	−1
		(−1)	( 1 )
		0	0
		1		2
		(−1)		(−2)
		0		0
		0		0
		1 −1 0 0 ( 0 )
		1 −1 0 0 0 ( 0 )

2. ACTIVIDAD: “Completar las tablas de información de los grafos K3,m”

· Observando lo obtenido anteriormente, redactar conjeturas acerca de las matrices de laplacianas y sus autovalores, para cualquier valor de “m”.

Actividades a trabajar en grupos, en gabinete de informática; o individualmente

Tabla 4. Matrices laplacianas y de adyacencia de grafos K3,m
Grafo K3,m	Matriz Laplaciana	Valores Propios	Matriz de Adyacencia	Valores Propios	Gráfica
m=1		{0, 4, 1, 1}
m=2		{0, 5, 3, 2, 2}
m=3		{0, 6, 3, 3, 3, 3}
m=4

3. ACTIVIDAD: genere tabla 5, (ídem lo realizado en Tabla 2), que permita el estudio de Vectores propios de Matrices Laplacianas de grafos K3,m.

4. ACTIVIDAD: genere tabla 6, (ídem lo realizado en Tabla 3), que permita el estudio de Vectores propios de Matrices Adyacencia de grafos K3,m.

El uso del recurso tecnológico Geogebra aplicado al proceso de enseñanza - aprendizaje de la matemática, su importancia radica que es una herramienta dinámica que permite ganar tiempo al estudiante, para hacer múltiples ensayos en el tiempo de solo un desarrollo realizado con lápiz y papel, esto provee de una capacidad de análisis, mejora significativamente la motivación en los estudiantes y a la vez promueve la autonomía en ellos en contextos educativos Coloma (2020), Zabala (2012), Real (2013).

Sanclair y Yurita (2008) realizan investigaciones de cómo las TIC hace mejorar las conjeturas y los razonamientos en cualquier problema. Alemán de Sánchez (2002) señala las ventajas teóricas del uso de las TIC en las matemáticas, entre otros.Una competencia que el estudiante debe desarrollar es: “Tratamiento de la información y competencia digital”.

5. ACTIVIDAD: “Genere y Complete tablas de información de los grafos K4,m” ( similares las trabajadas en las actividades previas)

RESULTADOS

Como es una actividad en desarrollo, se plantea como se espera que el estudiante llegue a los resultados esperados:

Segunda Parte: Elaboración de Conjeturas

Proceso 1: esta es la etapa de búsqueda de patronesdesde el análisis de conjeturas, en base a lo recabado en las tablas anteriores, se inicia el trabajo sobre los autovalores de matrices laplacianas.

1. ACTIVIDAD: para trabajaren conjeturas de lo visualizado en los autovalores de la matriz Laplaciana de K2,m.

· Es el “cero” autovalor las matrices laplacianas de K2,m ¿ Con qué multiplicidad algebraica?

· Son “m”,“m+2”, “dos”:autovalores de las matrices laplacianas de K2,m ¿ Con que multiplicidad algebraica?

· Hay algún otro autovalor distinto de los anteriores?, Se puede vincular su valor con algo de lo hallado?, que multiplicidad tiene?

· Tiene algún autovalor relación con el tamaño de la matriz?

· Indicar todos los autovalores de las matrices laplacianas de K2,6 ; K2,7, y K2,8

2. ACTIVIDAD: para trabajar en conjeturas de lo visualizado en los autovalores de la matriz Laplaciana de K3,m.

· Es el “cero” autovalor las matrices laplacianas de K2,m ¿ Con qué multiplicidad algebraica?

· Son “m” ,“m+3” ,“tres” :autovalores de las matrices laplacianas de K2,m ¿ Con que multiplicidad algebraica?

· Hay algún otro autovalor distinto de los anteriores?, Se puede vincular su valor con algo de lo hallado?, que multiplicidad tiene?

· Tiene algún autovalor relación con el tamaño de la matriz?

· Indicar todos los autovalores de las matrices laplacianas de K3,6 ; K3,7, y K3,8

3. ACTIVIDAD: plantee trabajo similar a las dos actividades anteriores para responder con lo visualizado, en los autovalores de la matriz Laplaciana de K4,m.

Proceso 2: etapa de búsqueda de patrones desde el análisis de conjeturas, en base a lo recabado en las tablas anteriores, se inicia el trabajo sobre los autovalores de la matriz de adyacencia.

1. ACTIVIDAD: para trabajar en conjeturas de lo visualizado en los autovalores de la matriz de adyacencia de K2,m.

· Son “cero” ,“√𝟐. 𝒎”, “-√𝟐. 𝒎”: autovalores de las matrices de adyacencia de K2,m ¿ Con qué multiplicidad algebraica?

· Hay algún otro autovalor distinto de los anteriores?

· Para los autovectores que trabajó, cuanto suman las componentes no nulas?.

· Cómo se disponen en el autovector, las componentes nulas y no nulas?

2. ACTIVIDAD: para trabajar en conjeturas de lo visualizado en los autovalores de la matriz de adyacencia de K3,m.

· Son el “cero” ,“√𝟑. 𝒎” ,“-√𝟑. 𝒎”:autovalores de las matrices de adyacencia de K3,m ¿ Con qué multiplicidad algebraica?

· Hay algún otro autovalor distinto de los anteriores?

· Para los autovectores que trabajó, cuanto suman las componentes no nulas?

· Cómo se disponen en el autovector, las componentes nulas y no nulas?

3. ACTIVIDAD: en base a las dos tareas previas, plantee conjeturas de lo visualizado en los autovalores de la matriz de adyacencia de K4,m.

Tercera Parte: Generalización de Conjeturas Respecto de Matrices Laplacianas

Proceso 1: generalización de las conjeturas, demostración de algunos patrones en base a lo recabado en la etapa anterior, se inicia el trabajo sobre el autovalorcero de la matriz Laplaciana de Kn, m.

· Sugerencia usar la observación sobre la estructura de las filas de la matriz Laplaciana y conclusiones del punto 8) de las actividades precedentes.

Proceso 2: generalización de conjeturas, demostración de que cero es autovalor de la matriz de adyacencia de Kn, m.

· Sugerencia armar un formato general del autovector, según lo visualizado en las tablas 2, 3, 5, y 6; de las actividades precedentes y probar que es autovector.

Aplicaciones a futuro

Cálculo de la energía de un grafo (Cubria, 2018), por uso de Matriz Laplaciana o por Matriz de Adyacencia y establecer vinculaciones con el número de ejes del grafo.

CONCLUSIONES

La experiencia desarrollada, permitirá que los alumnos compartan algo que hayan creado o descubierto. Dar un tiempo especifico para esa etapa de comunicación, fomenta la concentración, se pueden inspirar en las deducciones de sus compañeros y encontrarán valor en su propio trabajo (Eady&Lockyer, 2018). En este contexto se infiere que a menudo, los estudiantes que no sobresalen en las clases tradicionales no tienen la oportunidad de recibir muchos elogios. Por lo tanto, la tecnología cambia ese entorno, brindando oportunidades para que todos los estudiantes brillen, incluidos los introvertidos y aquellos que pueden carecer de competencia en ciertas materias al compartir sus ideas en clases. La integración de las TIC en matemática es realmente necesaria para motivar a los estudiantes y hacer las clases más innovadoras, promueven el aprendizaje autónomo y hacen que los encuentros sean más gratificantes.

La experiencia presentada, proporciona un amplio abanico de ventajas, las cuales se detallan en lo que sigue:

Ventajas del uso del software en la enseñanza-aprendizaje

· Beneficia a los estudiantes a que den primacía a los procesos de pensamiento sobre los procesos manuales, de hacer con lápiz y papel, para que puedan investigar y construir conocimiento matemático.

· En principio es conveniente trabajar con material manipulativoqueimplemente un software matemático, para reducir el volumen de cálculos a mano, antes de pasar al plano aritmético-algebraico.

· El trabajo con GeoGebra, conforma un gran apoyo académico, logrando una mejora significativa en el escenario tradicional del proceso de aprendizaje, adaptado a una problemática contextualizada.

Ventajas del trabajo algebraico,en el proceso de enseñanza-aprendizaje

· El trabajo con patrones y regularidades, alienta el desarrollo de distintos puntos de vista para abordar un problema, muestra que encontrar un enfoque no implica que él esté concluido e, incluso, permiten generar nuevos problemas. Conduce a reconocer el valor del lenguaje algebraico, tanto para expresar variables como para validar conjeturas, apoyándose en las reglas de transformación de escrituras.

· El trabajo con patrones conduce a hacer conjeturas, a simbolizarlas para luego en el proceso de generalización,demostrarlas y aplicarlas en soluciones y resultados a otros problemas.

REFERENCIAS BIBLIOGRÁFICAS

1. Alemán de Sánchez, A. (2002). La enseñanza de la matemática asistida por computador. Recuperado en Julio de 2019 de: https://es.scribd.com/document/7795982/La–Tecnologia–y–La–Mat

2. Castro, E., Cañadas, M. C. y Molina, M. (2010). El razonamiento inductivo como generador de conocimiento matemático. UNO, 54. Recuperado de: http://digibug.ugr.es/bitstream/10481/26079/6/Uno-54-_2010.pdf

3. Coloma, M. L. (2020). Las Tics como herramienta metodológica en matemática. Revista ESPACIOS Vol. 41 (11) , 1-9. Recuperado el 6 de 08 de 2020, de http://www.academia.edu/download/62945190/Articulo_Espacios_TICS20200413- 81578- 14jzkam.pdf

1. Cubria, F(2018). Energía de matrices. Tesis de maestría. Recuperado en Noviembre de 2023 de: https://www.fing.edu.uy/imerl/grupos/gia/pdf/fcubria_mas.pdf

2. Eady M., Lockyer L. (2018). Technology and teachingstrategies. Tools forlearning, vol 23. N° 4.

5. Herrera M., Izquierdo J., Pérez - García R. y Ayala-Cabrera D. La regularización del grafo de la red de abastecimiento de agua para la propuesta de su sectorización. ResearchGate. Recuperado de https://www.researchgate.net/publication/288965452_La_regularizacion_del_grafo_de_la_red_de_abastecimiento_de_agua_para_la_propuesta_de_su_sectorizacion

6. Joshua, J y Dupin, J. (2005). Introducción a la didáctica de las ciencias y de la matemática. Buenos Aires. Colihue.

7. Lesley L., Freiman V. (2004). Tracking primary student ś understanding of patterns. In Proceeeding of the 28thConference of the International Group for the Psychology of Mathematics Education (Vol. 2, pp. 415-422). Norway. PME.

8. Mañas, J. (2013). Utilización de las tic en el aula. GeoGebra y wiris. (Tesis de maestría). Universidad de Almería, España. Recuperado de http://repositorio.ual.es/bitstream/handle/10835/2289/Trabajo.pdf?sequence=1

9. Papic M. (2007). Promotting repeating patterns with Young children-more than just alternating colours. AustralianPrimaryMathemathicsClassroom, 12(1), 8.

10. Pochulu M. y Rodríguez M. (2016). Educación Matemática. Aportes a la formación docente desde distintos enfoques teóricos. Los Polvorines, Argentina. UNGS. Radford, L. (2013). En torno a tres problemas de la generalización. En: L. R.ico

11. M. C. Cañadas,J. Gutiérrez, M. Molina y I. Segovia (Eds.). Investigación en Didáctica de la Matemática. España: Editorial Comares.

12. Rangel Álvarez, L (2012) Patrones y Regularidades Numéricas: Razonamiento Inductivo. Universidad Nacional de Colombia, Colombia.

13. Real, M. (2013). Las TIC en el proceso de enseñanza y aprendizaje de las matemáticas. personal.us.es, 1-13. Recuperado el 3 de 08 de 2020, de https://personal.us.es/suarez/ficheros/tic_matematicas.pdf

14. Rodríguez, M. (2017). Criterios para valorar el uso de nuevas tecnologías en la clase de matemática. En P. Barreiro, P. Leonian, T. Marino, M. Pochulu y M. Rodríguez (Eds.), Perspectivas metodológicas en la enseñanza y en la investigación en educación matemática. (pp. 71 - 94). Los Polvorines, Argentina. UNGS.

15. Sinclair, N. y Yurita, V.(2008). To be or to become: How Dynamic geometry changes discourse. Research in: Mathematics Education, 10, 135-150.

16. UNESCO (2005). Formación docente y las tecnologías de Información y Comunicación, Santiago.

17. Zabala, S. Z. (2012). Pedagogía Informacional: Nuevo paradigma para educar en la sociedad de la información. recursos.portaleducoas.org, 1-18. Recuperado el 2 de 08 de 2020, de https://recursos.portaleducoas.org/sites/default/files/1757.pdf

18. Bhagat, P. K., Choudhary, P., & Singh, Kh. M. (2021). A novel approach based on fully connected weighted bipartite graph for zero-shot learning problems. Journal of Ambient Intelligence and Humanized Computing, 12(9), 8647–8662. https://doi.org/10.1007/s12652-020-02615-6

19. Blöcker, C., & Rosvall, M. (2020). Mapping flows on bipartite networks. Physical Review E, 102(5), 052305. https://doi.org/10.1103/PhysRevE.102.052305

20. Chakraborty, B., & Mandal, M. (2022). Regularity of symbolic powers of certain graphs (arXiv:2203.08572). arXiv. https://doi.org/10.48550/arXiv.2203.08572

21. Dung, L. X., Hien, T. T., Nguyen, H. D., & Trung, T. N. (2021). Regularity and Koszul property of symbolic powers of monomial ideals. Mathematische Zeitschrift, 298(3), 1487–1522. https://doi.org/10.1007/s00209-020-02657-8

22. Emadi Kouchak, M. M., Safaei, F., & Reshadi, M. (2023). Graph entropies-graph energies indices for quantifying network structural irregularity. The Journal of Supercomputing, 79(2), 1705–1749. https://doi.org/10.1007/s11227-022-04724-9

23. Habib, M., Mouatadid, L., Sopena, É., & Zou, M. (2024). (𝜶,𝜷)—Modules in Graphs. SIAM Journal on Discrete Mathematics, 38(1), 566–589. https://doi.org/10.1137/21M1443534

24. Habib, M., Mouatadid, L., & Zou, M. (2020). Approximating Modular Decomposition Is Hard. In M. Changat & S. Das (Eds.), Algorithms and Discrete Applied Mathematics (pp. 53–66). Springer International Publishing. https://doi.org/10.1007/978-3-030-39219-2_5

25. Hang, N. T., & Hien, T. T. (2023). Regularity of powers of cover ideals of bipartite graphs. International Journal of Algebra and Computation, 33(02), 317–335. https://doi.org/10.1142/S0218196723500169

26. Jin, Y., Zhang, W., He, X., Wang, X., & Wang, X. (2020). Syndrome-aware Herb Recommendation with Multi-Graph Convolution Network. 2020 IEEE 36th International Conference on Data Engineering (ICDE), 145–156. https://doi.org/10.1109/ICDE48307.2020.00020

27. Koley, M., & Römer, T. (2022). Seminormality, canonical modules, and regularity of cut polytopes. Journal of Pure and Applied Algebra, 226(1), 106797. https://doi.org/10.1016/j.jpaa.2021.106797

28. Lin, R. (2021). Conditional matching preclusion for regular bipartite graphs and their Cartesian product. Discrete Applied Mathematics, 299, 17–25. https://doi.org/10.1016/j.dam.2021.04.011

29. Megias, D., Alatrista Salas, H., Salas, J., Maehara Aliaga, Y., & Núñez del Prado, M. (2022). A graph-based differentially private algorithm for mining frequent sequential patterns. https://doi.org/10.3390/app12042131

30. Nandi, R., & Nanduri, R. (2022). On regularity bounds and linear resolutions of toric algebras of graphs. Journal of Commutative Algebra, 14(2), 285–296. https://doi.org/10.1216/jca.2022.14.285

31. Nandi, R., & Nanduri, R. (2023). On regularity of Rees algebras of edge ideals of cone graphs. Indian Journal of Pure and Applied Mathematics, 54(1), 28–37. https://doi.org/10.1007/s13226-022-00226-9

32. Nanduri, R. (2022). On regularity of symbolic Rees algebras and symbolic powers of vertex cover ideals of graphs. Proceedings of the American Mathematical Society, 150(5), 1955–1965. https://doi.org/10.1090/proc/15824

33. Neves, J. (2020). Regularity of the vanishing ideal over a bipartite nested ear decomposition. Journal of Algebra and Its Applications, 19(07), 2050126. https://doi.org/10.1142/S0219498820501261

34. Neves, J., Vaz Pinto, M., & Villarreal, R. H. (2020). Joins, ears and Castelnuovo–Mumford regularity. Journal of Algebra, 560, 67–88. https://doi.org/10.1016/j.jalgebra.2020.05.014

35. Nunez-del-Prado, M., Maehara-Aliaga, Y., Salas, J., Alatrista-Salas, H., & Megías, D. (2022). A Graph-Based Differentially Private Algorithm for Mining Frequent Sequential Patterns. Applied Sciences, 12(4), Article 4. https://doi.org/10.3390/app12042131

36. Shen, Y.-H., & Zhu, G. (2023). Powers of generalized binomial edge ideals of path graphs (arXiv:2310.20235). arXiv. https://doi.org/10.48550/arXiv.2310.20235

37. Wang, H., & Tang, Z. (2023). Regularity of powers of binomial edge ideals of complete multipartite graphs. Czechoslovak Mathematical Journal, 73(3), 793–810. https://doi.org/10.21136/CMJ.2023.0246-22

38. Wu, Y., Yin, Z., Zhou, K., Wang, R., Yang, Y., Yin, Z., Ruan, C., & Zhang, Y. (2021). A Hybrid-scales Graph Contrastive learning Framework for Discovering Regularities in Traditional Chinese Medicine Formula. 2021 IEEE International Conference on Bioinformatics and Biomedicine (BIBM), 1104–1111. https://doi.org/10.1109/BIBM52615.2021.9669658

39. Zhang, X., Wang, H., Yu, J., Chen, C., Wang, X., & Zhang, W. (2022). Polarity-based graph neural network for sign prediction in signed bipartite graphs. World Wide Web, 25(2), 471–487. https://doi.org/10.1007/s11280-022-01015-4

FINANCIACIÓN

Ninguna.

CONFLICTO DE INTERÉS

Ninguno.

CONTRIBUCIÓN DE AUTORÍA

Conceptualización: Elisa Oliva, Mathias Díaz.

Investigación: Elisa Oliva, Mathias Díaz.

Metodología: Elisa Oliva, Mathias Díaz.

Administración del proyecto: Elisa Oliva, Mathias Díaz.

Redacción-borrador original: Elisa Oliva, Mathias Díaz.

Redacción-revisión y edición: Elisa Oliva, Mathias Díaz.